A Gentle Introduction to Tensor

Introduction

 

As machine learning and deep learning are gaining popularity in the field of technology, there are a lot of concepts that are coming to light in a new way. I am sure most of us have heard about Tensors in mathematics. 

 

In scientific terms, a tensor is basically an algebraic object that defines the multilinear relationship between sets of algebraic objects related to a vector space. In other words, Tensor is that space which can accumulate data in N dimensions. They are used almost interchangeably with matrices, making them their generalizations to N-dimensional spaces.

---

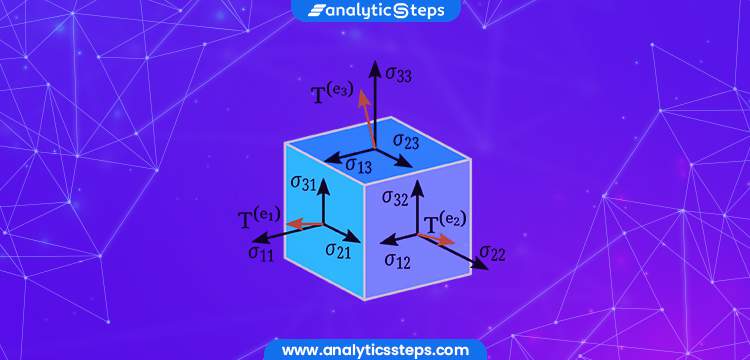
A second order Cauchy stress tensor, (source)

---

The diagram given above describes the stress forces that might be experienced by any material at a given point. Even though tensors are referred to by their components in a basis related to a particular coordinate system, they are defined as ‘independent’.

 

Tensors are often used in the field of mathematics and physics for finding solutions in the areas of mechanics, electrodynamics, relativity, etc. But these are not the only fields where tensors are used, they are also widely used in machine learning, deep learning and data structures. In this article, we are going to introduce Tensorflow and discuss Tensors for Deep Learning.

 

(Must check: Branches of discrete mathematics)

 

What is Tensor?

 

Tensor is a primary data structure that is used by neural networks for representing all the inputs, outputs and transformations occurring within them. A vector quantity is considered as a first-order Tensor and a matrix is considered as a second-order tensor. 

 

As per machine learning mastery, we can represent a tensor notation like:

 

        t111, t121, t131     t112, t122, t132      t113, t123, t133

T =  t211, t221, t231     t212, t222, t232      t213, t223, t233

        t311, t321, t331     t312, t322, t332      t313, t323, t333

 

Many operations that can be done with scalars, vectors, and matrices can also be done with tensors. In the field of mathematics, Tensors work more than a data container. They provide descriptions of valid linear transformations between tensors in addition to numeric data. The cross product and the dot product are two examples of such transformations or relations. 

 

Tensors can be thought of as things in an object-oriented sense, rather than merely as data structures, from a computer science perspective. Tensors can be of 0D, 1D, 2D, 3D, 4D and 5D. 3D tensors are used in time series, 4D tensors are used with images and 5D tensors are used with videos.

 

What is TensorFlow?

 

Google's flagship machine learning library for Tensors is called “TensorFlow”.  It is a framework that is developed and maintained by Google. It allows mathematical operations to be done on a CPU or GPU in a more efficient manner. Tensorflow is popular because of its flexibility and scalability. 

 

TensorFlow is the most popular deep learning library because it uses tensors for all the operations. In tensorflow, the programmer is required to build the graph first and then execute it. This allows the process to be tailored to the specific task at hand, significantly decreasing calculation time. It also allows the code to be run on more than one GPUs. 

 

(Must check: Best neural network software) 

 

Tensors in Machine Learning

 

Tensors in data structures can be scalars, vectors and matrices or the combination of all. They can be demonstrated using NumPy. Let us discuss some of the tensor transformations. 

 

The difference between a scalar, vector, matrix and tensors is depicted in the diagram below.

---

Different representation of matrices,source

---

1. Scalar:

 

A scalar is a single number and hence a 0-dimensional tensor. It has 0 axes. Even if a single number can be represented as a tensor, this does not imply that it should, or that it is in general. Although there are excellent reasons to be able to regard them as such, this ability can be perplexing as a storage method.

 

For example, 30 is a scalar of rank 0

 

2. Vector:

 

A vector is a one-dimensional (1D) tensor, which is more frequently referred to as an array in computer science. A vector is a set of integers with a single axis and a rank of one.

 

For example, a rank 1 vector is [ 4 5 2 1 1 6 ]

 

(Also check: R Programming vector functions)

 

 

3. Matrix:

 

A matrix is a tensor of rank 2. That means it has 2 axes. It is a 2 dimension tensor as the matrix is arranged as a grid of numbers. 

 

For example: [ [2 5 9]

  [5 4 1]

  [8 7 5]] 

 

(Related reading: Types of metrics in Linear Algebra)

 

 

4. 3D Tensor:

 

When we talk about tensors, we're usually referring to a generalisation of the idea of a matrix to N-3 dimensions. According to this source, the example of a 3D tensor is:

---

 

---

Tensor Element’s Operations

 

Tensors can be represented in python using N dimensional arrays, also called ndarray. Let us consider an example from machine learning mastery, of a 3x3x3 tensor as a NumPy ndarray. First the rows are defined and stacked as columns, then the list of columns stacked as levels in a cube.

---

Example:

# create tensor

from numpy import array

T = array([

  [[1,2,3],        [4,5,6],        [7,8,9]],

  [[11,12,13], [14,15,16], [17,18,19]],

  [[21,22,23], [24,25,26], [27,28,29]],

  ])

print(T.shape)

print(T)

---

There are many element-wise arithmetic operations that can be done between tensors in Python. Let us focus on the four main operations of the tensor, namely addition, subtraction, division and multiplication.

 

1. Tensor addition:

 

Two tensors with the same dimensions are added in order to create a new tensor with the same dimensions. Here, each of the scalar values of the resultant tensor is the element wise addition of the scalar elements in the main tensors. 

 

The basic formula for tensor addition is:

 

        a111, a121, a131     a112, a122, a132

A = a211, a221, a231      a112, a122, a132

 

        b111, b121, b131     b112, b122, b132

B =  b211, b221, b231     b112, b122, b132

 

C = A + B

 

        a111 + b111, a121 + b121, a131 + b131     a112 + b112, a122 + b122, a132 + b132

C = a211 + b211, a221 + b221, a231 + b231      a112 + b112, a122 + b122, a132 + b132

 

 

2. Tensor Subtraction:

 

When one tensor is subtracted element-wise from another tensor with the same dimensions, a new tensor with the same dimensions is created, with each scalar value being the element-wise subtraction of the scalars in the original tensors. The formula for tensor subtraction is:

 

        a111, a121, a131     a112, a122, a132

A = a211, a221, a231      a112, a122, a132

 

        b111, b121, b131     b112, b122, b132

B =   b211, b221, b231    b112, b122, b132

 

C = A - B

 

        a111 - b111, a121 - b121, a131 - b131     a112 - b112, a122 - b122, a132 - b132

C =  a211 - b211, a221 - b221, a231 - b231     a112 - b112, a122 - b122, a132 - b132

 

 

3. Tensor Division:

 

When one tensor is element-wise divided from another tensor with the same dimensions, a new tensor with the same dimensions is created, with each scalar value being the element-wise division of the scalars in the parent tensors. 

 

The formula for tensor division is:

 

        a111, a121, a131     a112, a122, a132

A = a211, a221, a231      a112, a122, a132

 

        b111, b121, b131     b112, b122, b132

B =   b211, b221, b231     b112, b122, b132

 

C = A / B

 

        a111 / b111, a121 / b121, a131 / b131     a112 / b112, a122 / b122, a132 / b132

C =   a211 / b211, a221 / b221, a231 / b231    a112 / b112, a122 / b122, a132 / b132

 

(Read also: Matrix Functions in R)

 

 

4. Tensor Multiplication:

 

Tensor multiplication or tensor product is denoted using a circle with a small x in the middle but for convenience, we will denote it as (x). When a tensor A has q dimensions and a tensor B has r dimensions, their product is a new tensor with the order of q + r or, to put it another way, q + r dimensions. 

 

The tensor product is not restricted to tensors; it can also be used to matrices and vectors, which might be an excellent place to start practising for higher-dimensional understanding.

 

• Tensor products for vectors:

 

a = (a1, a2)

 

b = (b1, b2)

 

c = a (x) b

 

       a1 * [b1, b2]

c =  a2 * [b1, b2]

 

• Tensor product for matrices:

 

        a11, a12

A =  a21, a22

 

        b11, b12

B =  b21, b22

 

C = A (x) B

 

                      b11, b12                    b11, b12

           a11 * (b21, b22)        a12 * (b21, b22)

C =                 b11, b12                    b11, b12

            a21 * (b21, b22),      a22 * (b21, b22)

 

(Suggested read: What is a confusion matrix?)

 

Conclusion

 

There are yet more complicated processes that necessitate higher-order tensors. Tensors are very important components and are used in many fields of mathematics, physics and technology. Tensor operations can be done with the help of python. In this article, we have discussed Tensors and tensorflow, and how tensors are used in element operations.