How Does Support Vector Machine (SVM) Algorithm Works In Machine Learning?

I assume that by now would have been familiar with linear regression and logistic regression algorithms. If you have not followed the same algorithm I would recommend you to go through them first before moving to support vector machines.

 

A support vector machine is a very important and versatile machine learning algorithm, it is capable of doing linear and nonlinear classification, regression and outlier detection. Support vector machines also known as SVM is another algorithm widely used by machine learning people for both classification as well as regression problems but is widely used for classification tasks. It is preferred over other classification algorithms because it uses less computation and gives notable accuracy. It is good because it gives reliable results even if there is less data. 

 

We will explain in this blog What is SVM, how SVM works, pros and cons of SVM, and hands on problem using SVM in python.

 

What Is Support Vector Machine (Svm)?

 

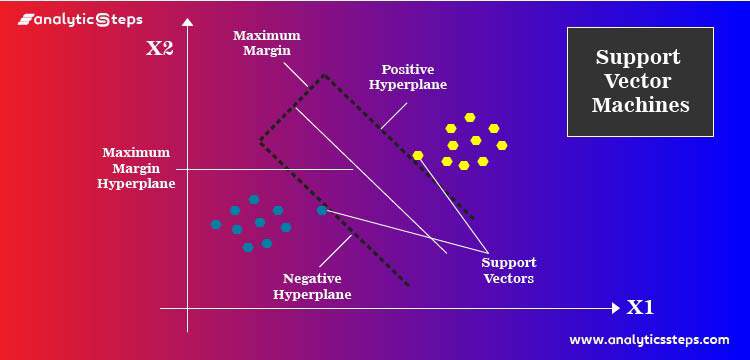
A support vector machine is a machine learning model that is able to generalise between two different classes if the set of labelled data is provided in the training set to the algorithm. The main function of the SVM is to check for that hyperplane that is able to distinguish between the two classes.

 

There can be many hyperplanes that can do this task but the objective is to find that hyperplane that has the highest margin that means maximum distances between the two classes, so that in future if a new data point comes that is two be classified then it can be classified easily. 

 

How Does Svm Works?

 

1. Linearly Separable Data

 

Let us understand the working of SVM by taking an example where we have two classes that are shown is the below image which are a class A: Circle & class B: Triangle. Now, we want to apply the SVM algorithm and find out the best hyperplane that divides the both classes.

---

Class A and B

---

Labelled Data

---

SVM takes all the data points in consideration and gives out a line that is called ‘Hyperplane’ which divides both the classes. This line is termed as ‘Decision boundary’. Anything that falls in circle class will belong to the  class A and vice-versa.

 

All hyperplanes are not good at classification

---

There can be many hyperplanes that you can see but the best hyper plane that divides the two classes would be the hyperplane having a large distance from the hyperplane from both the classes. That is the main motive of SVM to find such best hyperplanes.

 

There can be different dimensions which solely depends upon the features we have. It is tough to visualize when the features are more than 3.

 

Class A- Red & Class- B Yellow

---

Consider we have two classes that are red and yellow class A and B respectively. We need to find the best hyperplane between them that divides the two classes. 

Soft margin and hyperplane

---

Soft margin permits few of the above data points to get misclassified. Also,it tries to make the balance back and forth between finding a hyperplane that attempts to make less misclassifications and maximize the margin.

 

2. Linearly Non-separable Data

 

Linearly non-separarable dataset

---

If the data is non linearly separable as shown in the above figure then SVM makes use of kernel tricks to make it linearly separable. The concept of transformation of non-linearly separable data into linearly separable is called Cover’s theorem - “given a set of training data that is not linearly separable, with high probability it can be transformed into a linearly separable training set by projecting it into a higher-dimensional space via some non-linear transformation”. Kernel tricks help in projecting data points to the higher dimensional space by which they became relatively more easily separable in higher-dimensional space.

 

Kernel Tricks: 

 

Kernel tricks also known as Generalized dot product. Kernel tricks are the way of calculating dot product of two vectors to check how much they make an effect on each other. According to Cover’s theorem the chances of linearly non-separable data sets becoming linearly separable increase in higher dimensions. Kernel functions are used to get the dot products to solve SVM constrained optimization.

 

SVM Kernel Functions:

 

Kernel Functions | Credit: Source

---

While using the svm classifier we can take the kernel as ‘linear’ , ’poly’ , ‘rbf’ , ‘sigmoid’. Let us see which are the most used kernels that are polynomial and rbf (Radial Basis Function). You can refer here for documentation that is present on sklearn.

 

• Polynomial Kernel-  The process of generating  new features by using a polynomial combination of all the existing features.

• Radial Basis Function(RBF) Kernel-  The process of generating new features calculating the distance between all other dots to a specific dot. One of the rbf kernels that is used widely is the Gaussian Radial Basis function.

 

Recommended Blog: Introduction to XGBoost Algorithm for Classification and Regression

 

Degree of tolerance in SVM 

 

The penalty term that is passed as a hyper parameter in SVM while dealing with both linearly separable and non linear solutions is denoted as ‘C’ that is called as Degree of tolerance. Large value of C results in the more penalty SVM gets when it makes a misclassification. The decision boundary will be dependent on narrow margin and less support vectors.

 

 

Pros of SVM

 

• High stability due to dependency on support vectors and not the data points.

• Does not get influenced by Outliers. 

• No assumptions made of the datasets.

• Numeric predictions problem can be dealt with SVM.

 

 

Cons of SVM

 

• Blackbox method.

• Inclined to overfitting method.

• Very rigorous computation.

 

 

Hands On Problem Statement

 

We will take breast cancer dataset from the sklearn library, we will be implementing support vector machine and will find the accuracy for our model. SVM is generally preferred for smaller datasets as they turned out to be more accurate than any other regression technique.

 

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn import datasets
cancer = datasets.load_breast_cancer()
print("Labels: ", cancer.target_names)

 

---

STEPS: 

• Imported necessary libraries.

• Imported dataset that is “load_breast_cancer()”

• Printed Labels

---

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, test_size=0.4,random_state=99)
classifier = svm.SVC(kernel='linear')
 
classifier.fit(X_train, y_train)
y_pred = clf.predict(X_test)
from sklearn import metrics
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

 

---

• Splitted the dataset using train_test-split from sklearn.

• For evaluation of the model imported accuracy_score 

• Initiated object for SVC that is svc_model and fitted the training data to the model. Used ‘linear’ as a kernel.

• Made a prediction on y_test and calculated accuracy score on test data 

            that came out to be 96%.

 

Conclusion

 

In this blog, I have tried to explain to you about the support vector machine and how it works. I have talked about linearly as well as non linearly separable data, also discussed kernel tricks, kernel functions and degree of tolerance in SVM. At last I talked about the pros and cons of Support Vector Machine followed by a hands on problem statement on breast cancer dataset.

 

Recommended blog: Introduction to Decision Tree Algorithm in Machine Learning