What are Model Parameters and Evaluation Metrics used in Machine Learning?

Do you know how you can define a good machine learning model? There are different factors that decide about the performance of the model. A model is considered to be good if it gives high accuracy scores in production or test data or is able to generalize well on an unseen data. If it is easy to be implemented in production or scalable. 

 

Model parameters decide how to modify input data into respective output whereas the hyperparameters are used to regulate the form of model in use. Almost all common learning algorithms have attributes of hyperparameter that must be initialized before the training of the model.

 

What are Highly Accurate & Generalizable Model?

 

Models that are neither overfit and nor underfit are considered to be good models. The models that have less minimal bias and variance errors are called Right fit models.

 

How to check whether the model has minimal bias and variance error? 

 

You can estimate the accuracy for both training and testing simultaneously. You cannot be dependent only upon a single test to check about the performance of the model. As there are not multiple test sets, usage of K- fold cross validation and bootstrapping sampling to imitate multiple test sets.

 

What are Modeling Errors?

 

Modeling errors are defined as those sort of errors that reduce the power of prediction. There are mainly 3 different types of modeling error that are stated below:

 

1. Bias Error: This is the type of error that can occur anytime during the different stages or modeling from the initial data collection stage. It can occur during  analysis of the data available that decides the features. Also, while splitting the data into training, validation and testing. Due to class size there can be bias error, algorithms get influenced by the class that is more in number compared to other classes.

 

2. Variance Error: It is defined as the variance that is seen in the behavior of the model. Based on sample a model will execute distinctly on different samples. If the features or the attributes are increased in a model variance will also get increased that is because of the degree of freedom for the data points.

 

3. Random Errors: These are the errors that are caused due to unspecified factors.

 

 

How to define the performance of a model?

 

There are mainly three categories in which performance of a model is kept that are called as Rightfit, Underfit and Overfit models. Let us see what are these categories one by one.

 

• Rightfit models: Models that are able to generalize well and perform well in production are called Right Fit models. Models are able to classify well if they have continuous variability. Also, a model that is good at generalizing should neither be overfit nor underfit at the training data.

 

• Underfit model: These are the models where independent and target features interconnect in a linear way that means they are able to express in linear form. These models fail to apprehend the complex interlinkage between the features in the real world. These models are unable to generalize. 

 

• Overfit model: Models that execute very well in the training data are called as overfit models. They are complex polynomial surfaces that deform and change in the feature space to detach the classes. They are adaptable to the variance errors and cannot classify in the real world.

 

How to validate your model?

 

Validation of a model is like checking how good the model is performing. It is no guarantee if your model is performing really good in the training phase means it will also perform good in production. If you need to validate your model you always need to split out your data into two segments where the first segment takes care of the training data and another as a testing data to validate the model. 

 

In many cases, it is seen that we do not have sufficient data that can be splitted into train and test. Hence, to check the error made by the model on the test data might not be the good approach to estimate the error in the production data. In cases, where you do not have much large data, there can be various different techniques that can be made in use to evaluate the model error in production. One of such techniques is called "Cross Validation".

 

 

What is Cross validation?

 

• Cross-validation is a method to evaluate the model and check its performance on the unseen data.

• The model is created and evaluated multiple times.

• How many times the evaluation will be done will be dependent on the user. User needs to decide a value that is called as “k” which is an integer value.

• The sequence of steps used is repeated as many times as the value of ‘k’.

• Initially, for doing cross validation you need to use random functions to divide the original data into different folds.

 

Steps of Cross validation?

 

1. Randomly shamble the data.

2. Split your data into desired k folds.

3. For each different fold: 

• Retain the fold data that has been divided.
• Make use of the remaining data as a single training data.
• Fit model on the training data and validate on the test data.
• Keep the validation score and reject the model.
• Repeat the whole above steps.

 

4. These steps will continue going on k times.

5. Sum up the scores and take mean by dividing the sum by k.

6. Examine the mean score, the distribution to validate the performance of the model in the unseen data that is production data.

 

Code implementation of K fold cross validation is shown in the below image.

---

from numpy import array
from sklearn.model_selection import KFold
data = array([3,6,9,12,15,18,21,24,27,30])
kfolds = KFold(10, True)
for train, test in kfolds.split(data):
    print('Training Data: %s,Testing Data: %s' % (data[train], data[test]))

 

Code Implementation

---

K is a fundamental number. The minimum values that should be assigned to k should be 2 and maximum values that can be assigned to k can be the total of data points also known as LOOCV. (Leave one out cross validation). There is no formula that can be used to select the value of k but k=10 is considered to be good.

 

Evaluation of the model in an iteration

 

• The model gets trained on (k-1) no of folds and is validated on the fold that is left in each iteration.

• Mean Square error is calculated on fold that is left.

• As operation of cross val gets repeated k times so there are k times MSE’s that are computed. The expected overall MSE is calculated by taking the average of all MSE and dividing it by k.

 

To see the whole documentation about K fold cross validation you can refer here.

 

What is BootStrap Sampling?

 

It is defined as the technique that is used when we have very small volumes of data or limited data. To create data from the original data random function is used. Within the data, there can be repeated data due to identical records. The records that are not randomly taken are used for the testing purpose and that are always unique.

 

Consider we have 20 data points in the data then we can create different data having each 20 data points or less and respective test data. The data that is created might be only 20 or else less than or more than 20. More the data we create from a lesser volume of data, the more similar the generated data would be if we talk about data points.

 

An example of Bootstrap sampling is shown in the below image - 

---

from sklearn.utils import resample
 
data = [0.4, 0.8, 1.2, 1.4, 1.8, 2.2]
bootstrap = resample(data, replace=True, n_samples=6, random_state=1)
print('Bootstrap Sample: %s' % bootstrap)
oob = [x for x in data if x not in bootstrap]
print('OOB Sample: %s' % oob)

 

Code Implementation

---

• With the bootstrap data we can make models on the training and test and can take mean out of all the scores over all the iteration.

• Each iteration gives out a performance score while testing the model on bootstrapped data.

• These performance scores incline to follow normal distribution when there is an increase in the number of iterations.

• The distribution becomes normal for a very large number of iterations, also called as Central Limit Theorem.

 

Central Limit theorem states “the sampling distribution of the sample means approaches a normal distribution as the sample size gets larger — no matter what the shape of the population distribution.”

 

Different metrics that are used to measure performance of the model

 

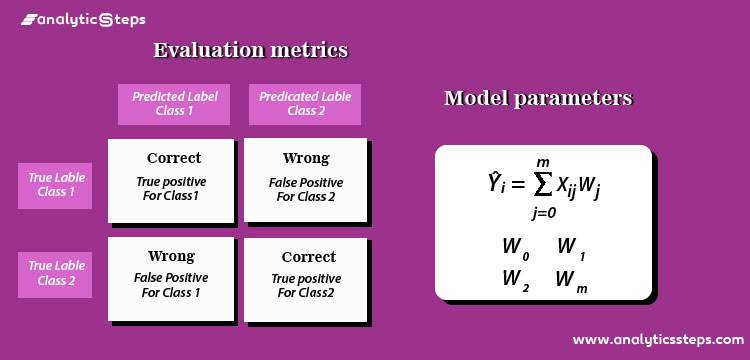
1. Confusion Matrix: It is defined as 2*2 matrix that tells about the performance of the model.

 

Confusion Matrix

---

2. Accuracy: It is defined as the score that is generated while generalizing the class. How accurately the model is able to generalize. 

 

Accuracy = (TP + TN) / (TP + TN + FP + FN)

 

3. Recall :  How much the model has predicted true data points as true data points is defined by the recall. 

 

Recall = (TP/TP+FN)

 

4. Precision: It tells about the positive data point recognized by the model, how many are actually positive.

 

Precision = (TP/TP+FP)

 

5. Specificity: It tells about the negative data point recognized by the model, how many are actually negative.

 

Consider a case where we are predicting diabetic patients and non diabetic patients. In this binary classification, diabetic patients are the class that is of interest and is labelled as positive (1) and other class as negative (0).

 

• True Positive (TP):  Cases where positive class is predicted as positive by the model. Ex- Diabetic patient (1) has been predicted as (1).

• True Negative (TN): Cases where negative class is predicted as negative by the model. Ex- Non-diabetic patient predicted as non diabetic.

• False Positive (FP): Cases where class was negative(0) but the model predicted as positive. Ex- Non-diabetic class(0) but predicted as diabetic. (1)

• False Negative (FN): Cases where class was positive but was predicted as negative. Ex- Diabetic class(1) but predicted as non-diabetic.(0)

 

Ideal situation is when all negative is predicted by the model as negative and positive as positive but practically this is not possible. There will exist false negative as well as false positive. The aim should always be to minimize but if you would minimize one other one would increase and vice versa! So it is suggested to minimize either of them.

 

Read more about different evaluation scores given in the sklearn library here.

 

Receiver Operating Characteristics (ROC) Curve

 

• It is a graphical representation of a curve that tells about the classifier performance.

• Graph that is plotted between TP and FP. (Total positive vs total negative)

• The point (0, 3.5) presents a perfectly classified class that is X.

• Classifiers that are nearer to Y axis and close to X axis(downwards) are stern in generalizing.

---

ROC Curve

---

If you want to see the documentation of roc curve that is there is sklearn you can visit here.

 

 

Conclusion

 

I conclude the blog by stating that a good model is never defined as the model with high accuracy, it should be able to generalize well in production. 

 

In this blog, I have discussed the machine learning model’s performance, how to define a good machine learning model, different modeling errors, performance of the model, validation of model, cross validation technique, bootstrap sampling and lastly different evaluation metrics that are used to validate the models and also discussed about roc curve.